Emettitore comune - MMETFT

Analisi della configurazione ad emettitore comune di un BJT

Partiamo con l'analisi della configurazione CE senza degenerazione di emitter in quanto, la resistenza sull'emettitore risulta by-passata dalla capacità CE come risulta visibile nella figura seguente.

Procedendo con l'analisi per piccoli segnali (le capacità dal punto di vista del segnale risultano dei corto circuiti) si ottiene il circuito di figura:

La tensione 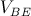è quella tra base ed emettitore mentre la tensione di uscita Vout prelevata sul collettore è data da:

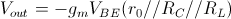
Applicando il teorema di Thevenin nei punti contrassegnati dalle "x" si ottiene il circuito semplificato di figura:

dove e .

Indicando con 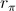la 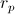di figura, posso calcolare la differenza di potenziale tra base ed emettitore e cioè:

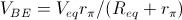
ottenendo così .

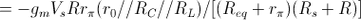In definitiva il guadagno di tensione è dato da:

.

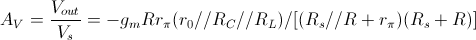Per il calcolo della resistenza di ingresso dello stadio considero il seguente schema è un generatore di tensione costante, fittizio:

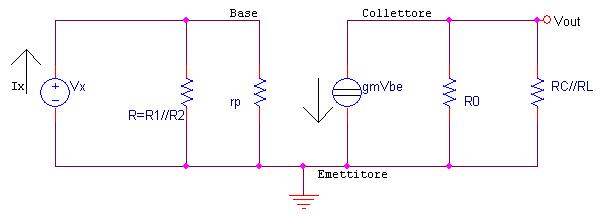
Poichè 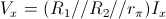la resistenza vista in ingresso sarà:

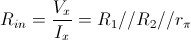
Considerando anche la resistenza del generatore di segnale si ha in definitiva:

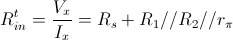
Per il calcolo della resistenza di uscita invece, pongo in corto circuito il generatore di segnale di ingresso e collego il generatore fittizio 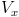come indicato nella figura seguente:

Poichè la tensione 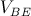è nulla, il generatore controllato sulla maglia di uscita, si comporta come un circuito aperto, per cui essendo 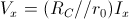la resistenza vista in uscita sarà:

Considerando anche la resistenza di carico RL, si ha in definitiva:

Vediamo ora come varia il guadagno introducendo la degenerazione di emitter. Si ottiene lo schema della figura seguente dove ho già applicato il teorema di Thevenin e ho sostituito 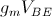con 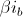, essendo:

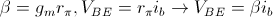
Dalla figura noto che la corrente che scorre in 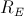è pari alla somma della corrente che scorre nella base e della corrente erogata dal generatore controllato che è quindi pari a 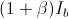. Proseguendo con l'analisi del circuito, scrivo l'equazione delle tensioni e delle correnti relative alla maglia composta da 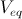, , 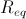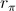ed :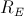

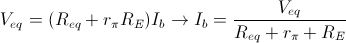
La tensione , tenendo conto del derivatore di corrente composto da ed 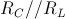è data da:

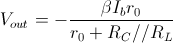
Sostituendo la calcolata precedentemente ottengo:

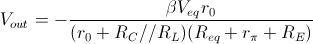
Per cui sostituendo il valore calcolato di 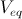ed 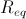si ottiene:

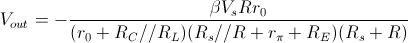
Quindi il guadagno di tensione sarà:

Per il calcolo della resistenza di ingresso dello stadio considero il seguente schema:

Considerando il derivatore di corrente costituito da , 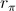ed 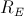la corrente è data da:

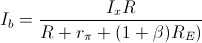
essendo anche 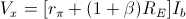, sostituendo il valore di calcolato precedentemente si ottiene:

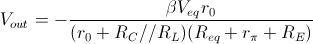
per cui:

e considerando anche la resistenza del generatore di segnale 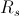, si ha in definitiva:

Per il calcolo della resistenza di uscita come prima, pongo in corto circuito il generatore di segnale di ingresso e collego il generatore fittizio 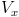come indicato nella figura seguente:

Osservando la parte finale dello schema si ricavano subito le seguenti relazioni:

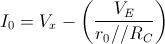
Osservando la maglia di ingresso noto subito che:

Per l'equilibrio delle correnti sul collettore si ha che 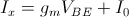, mentre l'equilibrio al nodo contrassegnato con 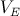, si ha che 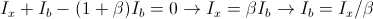. Quindi:

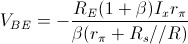
dalle quali si ottiene:

e portando tutti i termini in cui compare a sinistra e lasciando 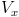a destra del segno uguale ottengo:

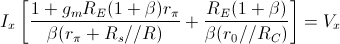
La resistenza vista in uscita sarà quindi:

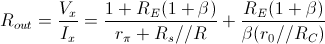
Tenendo conto anche del contributo relativo al carico 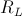, si ha la resistenza di uscita totale:

Dalle precedenti relazioni è possibile notare come la 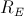influisce sulla resistenza di uscita e di ingresso aumentandone il valore. In genere la configurazione ad emettitore comune è utilizzata come stadio di ingresso in un amplificatore di tensione in quanto, come detto prima, presenta un'alta impedenza di ingresso. D'altra parte questa configurazione presenta l'inconveniente di avere un'alta resistenza di uscita che può essere risolto facendo seguire uno stadio a collettore comune (emitter follower).